Computer Science

Computer Science

 I love writing software. Currently, I'm focusing on learning fundamentals of C++, Algorithms and Linux/Unix shell scripting. See examples below:

Master the Mainframe Competition by IBM




I'm currently learning COBOL (Common business-oriented language) course on IBM.
The code is a very simple "Hello World" using Visual Studio and the extension "Zowe Explorer and IBM Z Open Editor".




Algorithms

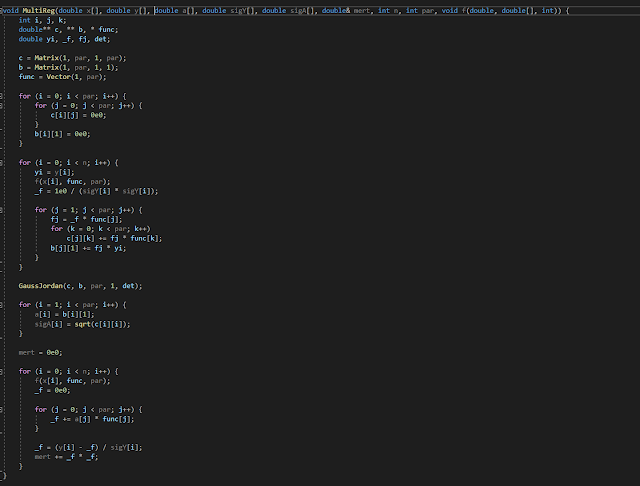
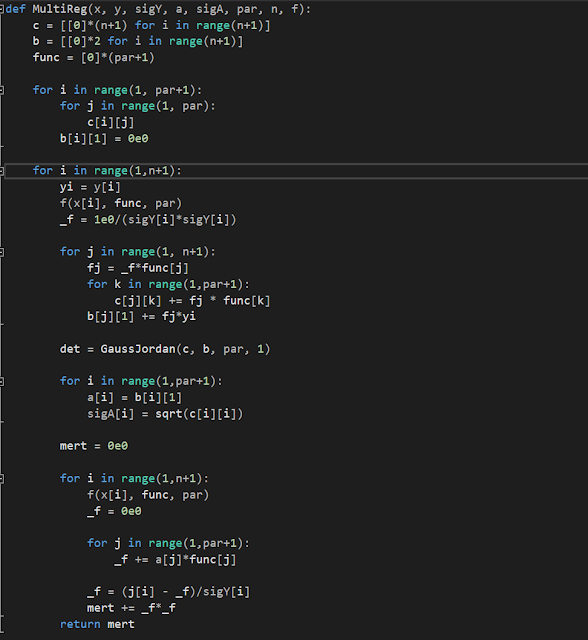
Multilinear regression

Multilinear regression is to fit a model represented by a linear combination of arbitrary functions of x to a set of observed data points.
The basis function Fj(x) most commonly will have the family of integer powers which the regression is based on.

In the code: 
x[] and y[] will be the x and y coordinates of the observed data.
n will be the number of observed data points
sigY[] will be the standard deviations of the observed data.
par will be the number of model parameters
a[] holds the parameters of the model
sigA[] will hold the uncertainties associated with the model parameters.
mert is the value of the Chi-square merit function.
f() is the user function.




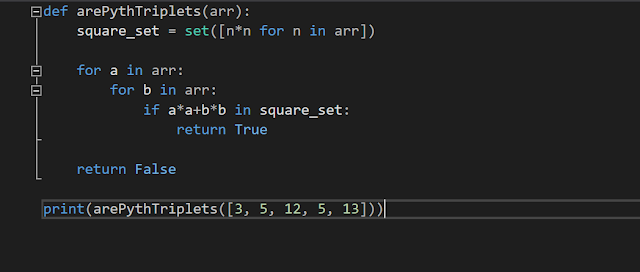
Pythagorean triplets


This problem requires you to find the Pythagorean triplets of an array.

Coded in C++ and Python.








Open Stack

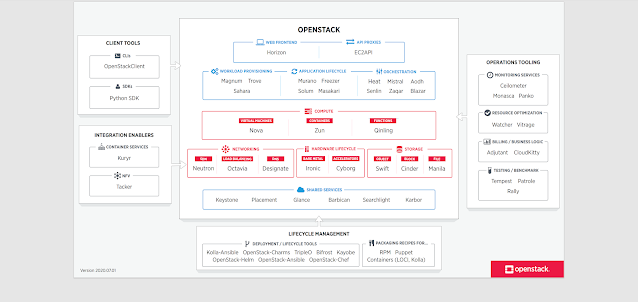
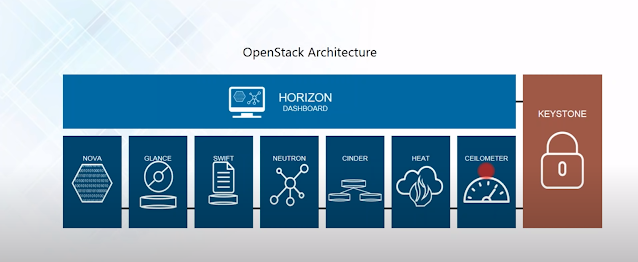
Openstack architecture:
Openstack is a cloud computing platform and can be found here: https://www.openstack.org 





Neville's Interpolation
Neville's interpolation method for tabulated functions is an optimized algorithm for constructing
the unique Lagrange interpolation polynomial for a given set of data points. It provides an error estimate as well.

Coded in C++ and Python.






FINDING EIGENVALUES: The Jacobian Method


Code example



CREATING C++/CLR WINDOWS FORMS FOR VISUAL STUDIO 2019

Step-by-step tutorial


Levenberg-Marquardt

Levenberg-Marquardt a.k.a. damped least-squares method in which you fit any arbitrary model function to observed data points, but requires the solution of the systems of nonlinear equations for determining the optimal model parameters.




Multilinear Regression


Pythagorean Triplets

https://motifsbyvincent.blogspot.com/p/pythagorean-triplets.html

 Sorting

Insertion sort: 



Bisectioning



False Positive



Hashing A String




Loading Textures From Files Using DirectX

This function loads a texture from a file using Direct X 9.
The reason the function is a boolean is because it is a good way to
check if the texture actually loaded.




 Attaching Mesh Components to an Actor in Unreal Engine 4

Simple C++ script in Unreal Engine 4 to attach a mesh component to an actor:

UStaticMeshComponent* helicopter;

 helicopter = CreateDefaultSubobject<UStaticMeshComponent>(TEXT("HELICOPTER"));
helicopter->SetupAttachment(RootComponent);
helicopter->bCastDynamicShadow = true;
helicopter->CastShadow = true;

 static ConstructorHelpers::FObjectFinder<UStaticMesh> BaseMeshAsset(TEXT(path_mesh));

 if (BaseMeshAsset.Object) {
    helicopter->SetStaticMesh(BaseMeshAsset.Object);
}


Linked Lists in Python and C++
I'm currently reviewing an essential data structure known as the linked list.
Coded in C++ and Python.



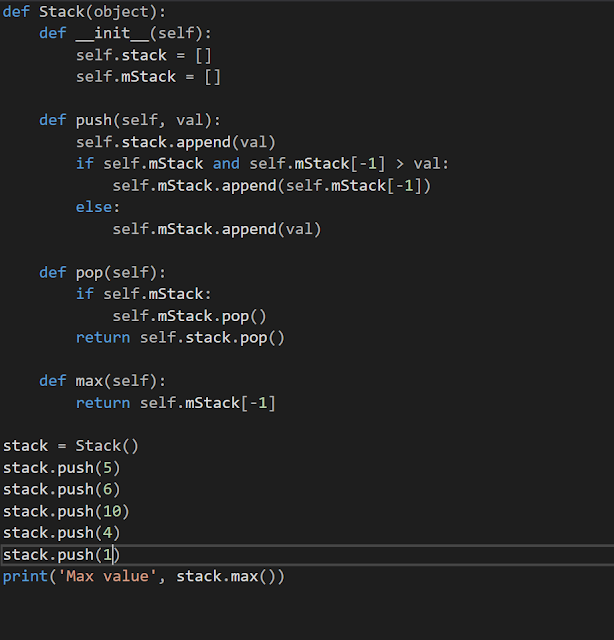
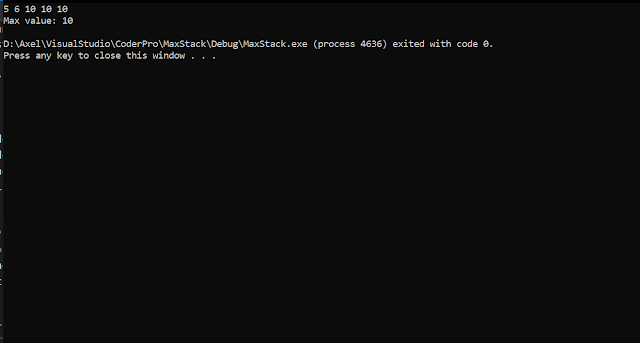
The Max Stack Algorithm

The goal of this problem is to find the maximum number in the stack: 5 6 10 4 1

Coded in C++ and Python.











Foundation of Algorithms
    Chapter 1:
    1: Write an algorithm that finds the largest number in an array.
    2: Write an algorithm that finds the smallest number in an array.
    3: Write an algorithm that prints out all the subsets of three elements of a set of n elements.
    4: Write an algorithm that finds the greatest common divisor of two integers.
    5. Big O and Omega notation problems
    (Solutions for 1-5)

     Chapter 2:
    Questions and my solutions

    1: Use recursive Binary Search to search for the integer 120 in the following list (array) 
       of integers.
    2: Suppose that, even unrealistically, we are to search a list of 700 million items 
       using recursive Binary Search. What is the maximum number of comparisons that this   
       algorithm must perform before finding a given item or concluding that it is not in the   
       list?
    3: Let us assume that we always perform a successful search. That is, the item x can 
       always be found in the list S. Improve Algorithm 2.1 by removing all unnecessary  
       operations.
    4: Show that the recurrence equation for W(n) is given by
       W(n) = 1 + W((n/2))
       W(1) = 1
    5: Suppose that, in Algorithm 2.1 (line 4), the splitting function is changed to 
       mid = low. Explain the new search strategy. Analyze the performance of this strategy   
       and show the results using order notation.
    6: Write an algorithm that searches a sorted list of n items by dividing it into three 
       sublists of almost n/3 items. This algorithm finds the sublist that might contain the 
       given item and divides it into three smaller sublists of almost equal size. The 
       algorithm repeats this process until it finds the item or concludes that the item is 
       not in the list.
    7: Use the divide-and-conquer approach to write an algorithm that finds the largest item
       in a list of n items.
    8: Use Mergesort to sort the following list.
       123 34 189 56 150 12 9 240
    9: Give the tree of recursive calls 
    11: Write an Mergesort algorithm
    12: Show that the recurrence equation for the worst-case time complexity for MergeSort is
        given by W(n) = W(n/2) + W(n/2) + n - 1 
    13: Given the recurrence relation
    14: Consider algorithm solve given below. This algorithm solves problem P by finding the   
        output (solution) O corresponding to any input I.
            
    15: Suppose that, in a divide-and-conquer algorithm, we always divide an instance of size 
        n of a problem into 10 substances of size n/3, and the dividing and combining steps
        take a time in Theta(n^2). Write a recurrence equation for the running time T(n),
        and solve the equation for T(n).
    16: Write a divide-and-conquer algorithm for the Towers of Hanoi problem. The Towers of
        Hanoi problem consists of three pegs and n disks of different sizes. The object
        is to move the disks that are stacked, in decreasing order of their size, on one of 
        the three pegs to a new peg using the third one as a temporary peg. The problem should 
        be solved according to the following rules:
        (1) When a disk is moved, it must be placed on one of the three pegs
        (2) Only one disk may be moved at a time, and it must be the top disk on one of the 
            pegs;
        (3) A larger disk may never be placed on top of a smaller disk.

        (a) Show for your algorithm that S(n)=2^n - 1.(Here S(n) denotes the number of steps
            (moves), given an input of n disks.)



    This is a printout of code that sent astronauts to the moon. It must have been exciting to be a programmer in the Apollo program.


    COMPUTER GRAPHICS

    Sometimes, I'm working on 3D modeling. Programming for 3D applications is really cool.

     

    Reviewing reference models in reality ...


    ...and here is the project on the Google drive...


    The Shipping Container Project



    Dump truck project...