The oscillations can be traced back to the large degree and number of zeros of the interpolant. To reduction of the polynomial degree
to a better degree can be done by having separate lower-degree interpolation polynomials on adjacent subintervals of the total interval.
Spline interpolation is a piecewise-polynomial approximation with interpolant restrictions.
The spline restrictions will be third-degree polynomials (cubic splines) with coefficients Ai, Bi, Ci, Di and can be determined from the
continuity and interpolation conditions at the interpolation nodes.
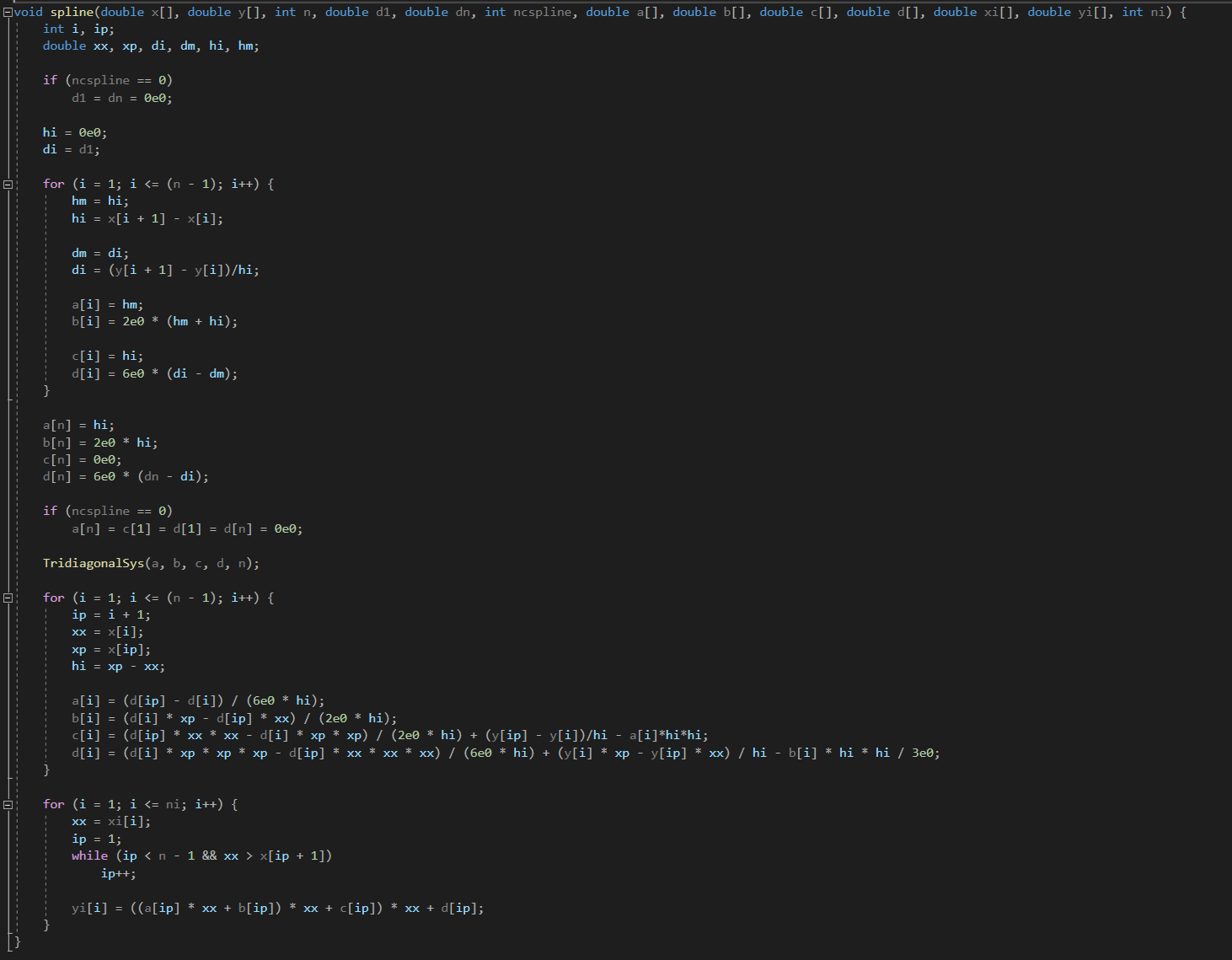
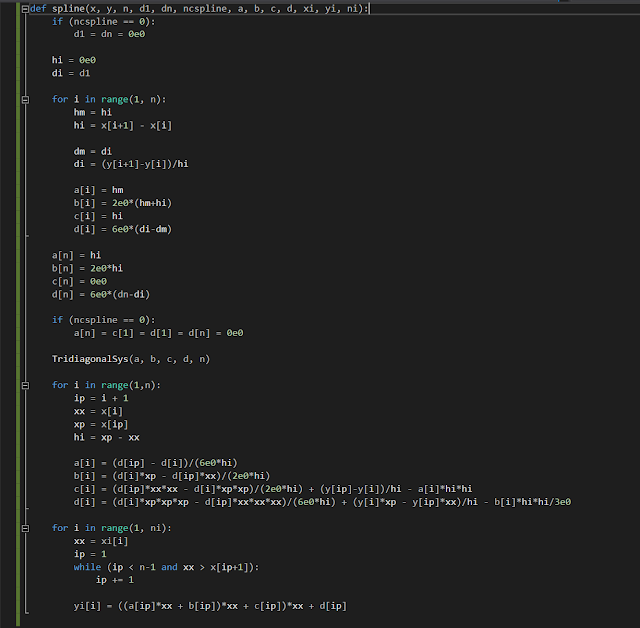
Code starts by obtaining the derivative coefficients and the 2nd derivatives will be stored in d.
Here we end up having a tridiagonal system having the solutions being the second derivatives d[i] of the splines at the interpolation nodes.
Obtaining coefficients Ai, Bi, Ci, Di comes from replacing the integration constants from the system for C'i and C''i back into the cubic splines.
Coded in C++ and Python.